Enhetsvektornotation | Vektorer och mellanslag | Linjär algebra | Khan akademin
När de förklarar dimensionen W representeras den som den negativa sidan av X-axeln. Varför är dimension W negativ X? Är det inte egentligen sin egen dimension?

- Försök att rita ett fyrdimensionellt diagram på en tvådimensionell yta. Det här är vad de kom på (din rätt men det är inte ett bra diagram).
Som @NendoTaka har nämnt är det ganska svårt att rita ett 4d-objekt på en 2d-yta.
Så här fungerar dimensionalitet:
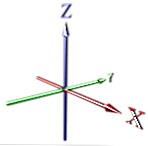
med en enda dimension skickas en punkt oändligt, vilket skapar en linje (se X)
i 2d lägger vi till en dimension vinkelrät mot den (se X, Y).
Sedan går vi vinkelrätt igen och expanderar uppåt för att få den tredje dimensionen (se X, Y, Z).
Eftersom 3d> 2d kan vi inte representera så bra på papper utan att lägga papperet eller lägga till fler ark ovanpå det - allt verkligen opraktiskt för visning på en skärm. Så istället använder vi perspektiv - hur våra ögon uppfattar 3d. Vanligtvis är vinklarna här ~ 30 grader.

Och det ser ganska okej ut, för våra ögon ser inte i denna traditionella 3d-mening, så härmar det som fungerar. Men när vi vill representera en fjärde dimension har vi inget att jämföra det med. Vi måste gå vinkelrätt igen och det är svårt för våra ögon att förstå eftersom vi inte har så mycket referens.
Här är ett exempel på en fjärde dimension:
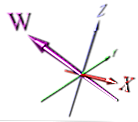
Detta är ett mer korrekt sätt att visa dimensionen, men det bygger fortfarande på perspektiv - det är inte direkt uppenbart att det är en ny dimension vid första anblicken.
Animatörerna valde antagligen att göra något enkelt som det skulle vara lättare att animera. Även om du roterar ovanstående bild kan X- och W-dimensionerna överlappa varandra - och detta skulle inte vara uppenbart i bilden utan pilpekare.
Så ja, de har fel - men det finns inte heller ett enkelt sätt att representera fyra dimensioner på ett enda pappersark
Koordinera bildkällor och läs bra
3- 1 För att vara rättvis finns det många vanliga sätt att projicera 4-dimensionella föremål som tesserakter och 3-sfärer i 3 dimensioner (och sedan ner till 2 dimensioner på vanligt sätt) som är mycket överlägsna den som används i showen, många av vilka har den extra bonusen att se coolare ut än den som används i showen.
- @senshin oh för säker, men jag antar att animatörerna också ville förklara något, snarare än att förbluffa
- 1 Du kan använda andra saker än position för att ange hur långt längs en axel något är, som färg.